Updates:
- 2024/01/26: published
- 2024/01/20: adding more examples and mounting tool/ruler
- 2024/01/15: starting write-up
Introduction
Since a while I was wondering how to create large(r) scale 3D prints like 1m / 1000mm or more, and I thought to use wood planks as slices and make “parametric wall” like sculptures. In order to get an idea of the procedure, I started with “parametric canvas” or Slices on Canvas.






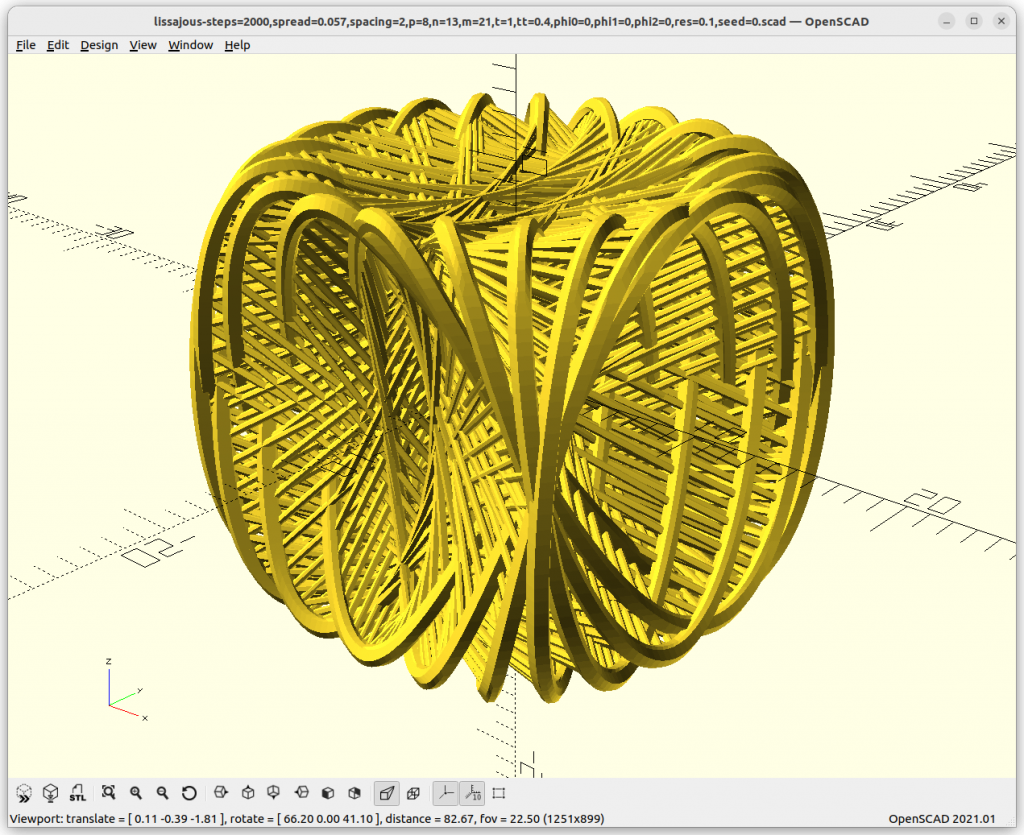
Models
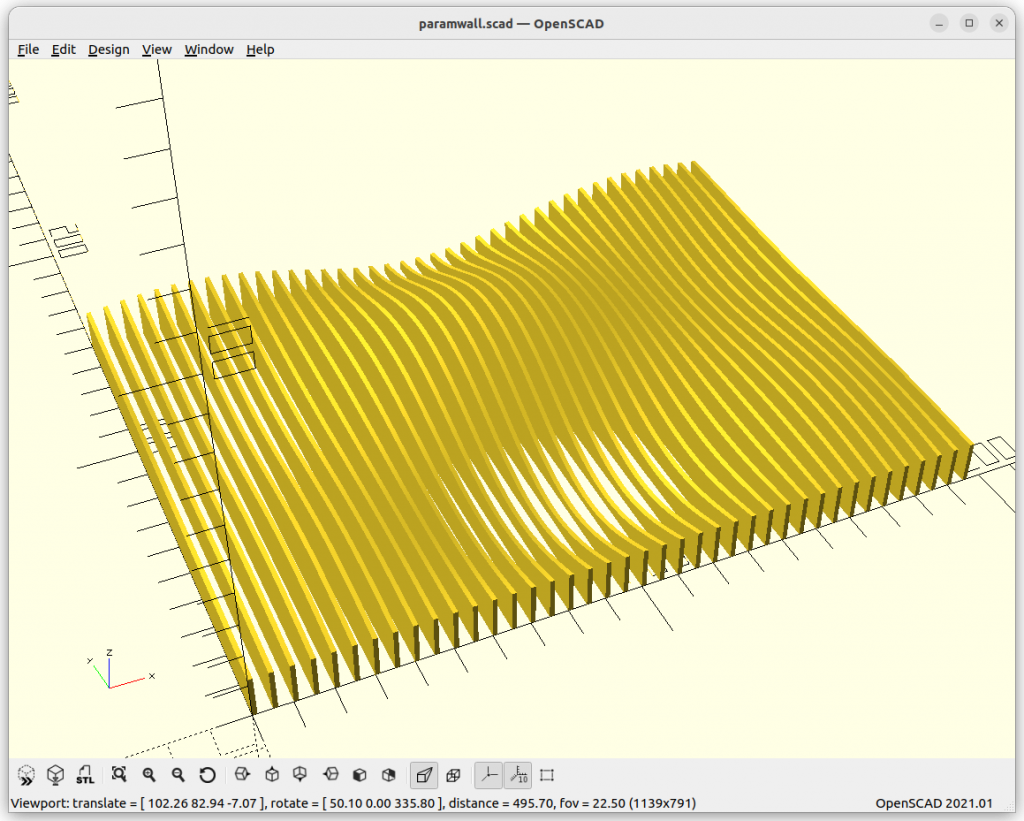
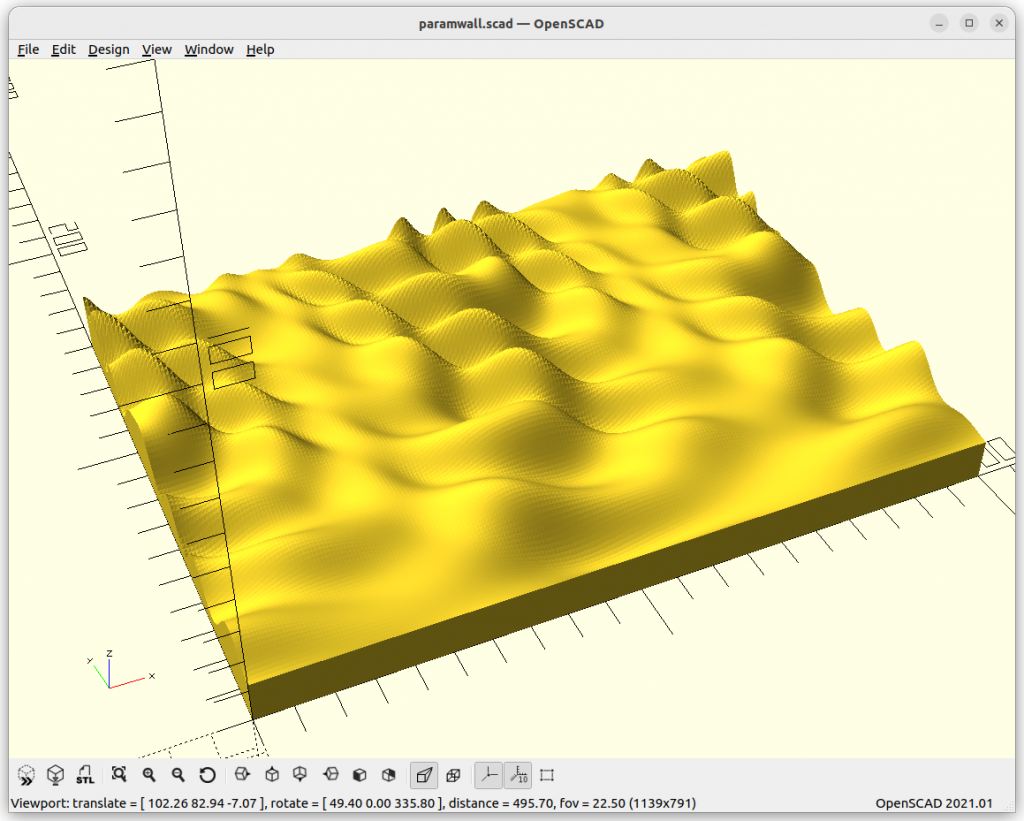
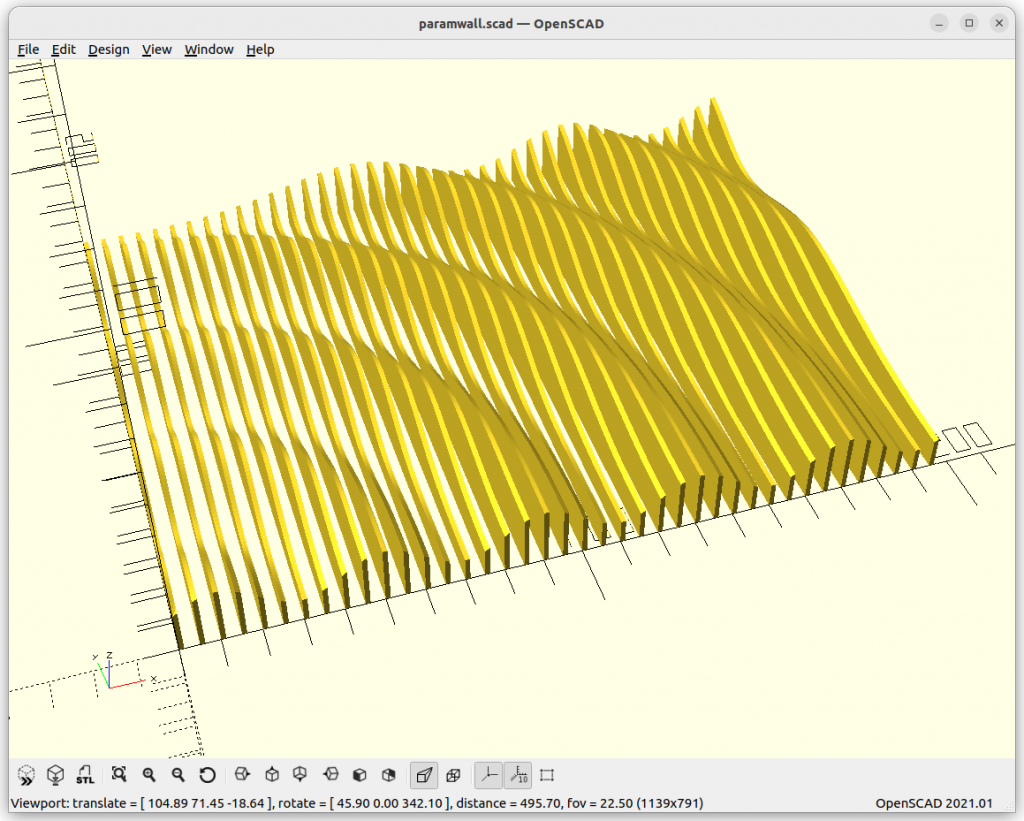
I used OpenSCAD to put together a few examples with 200×150 in size, and settled for 40 slices, which are then scaled up for 400x300mm canvas, the actual size is 340x240mm giving on each side 30mm margin to the edge of the canvas.
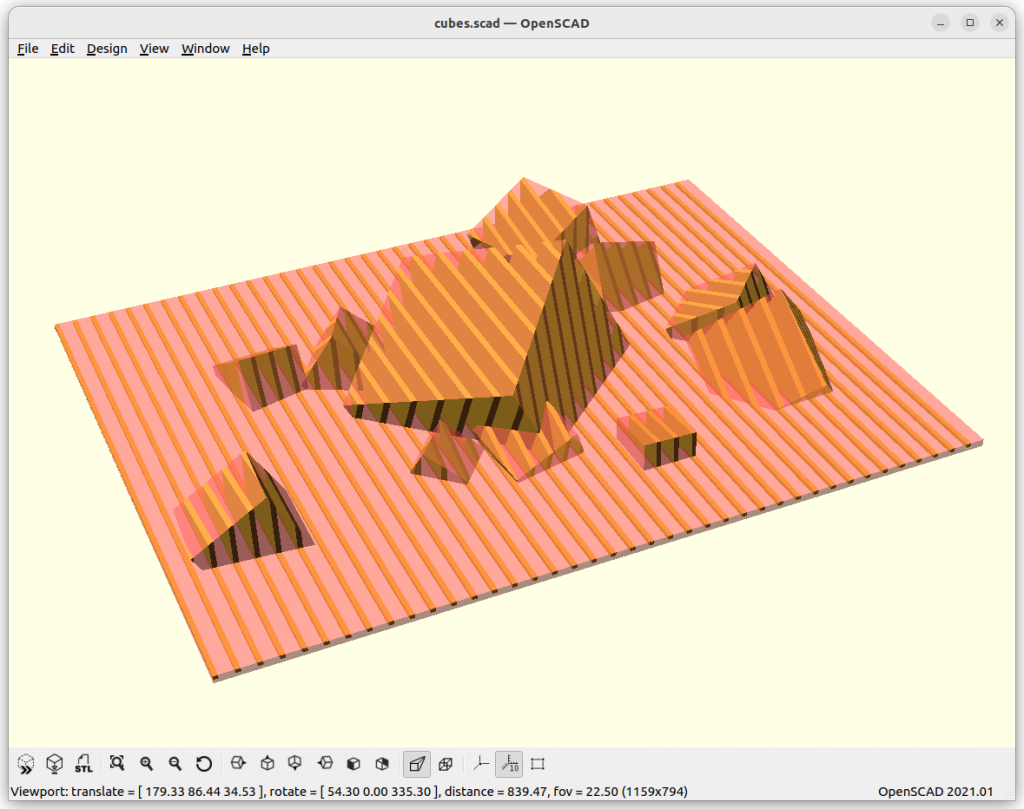
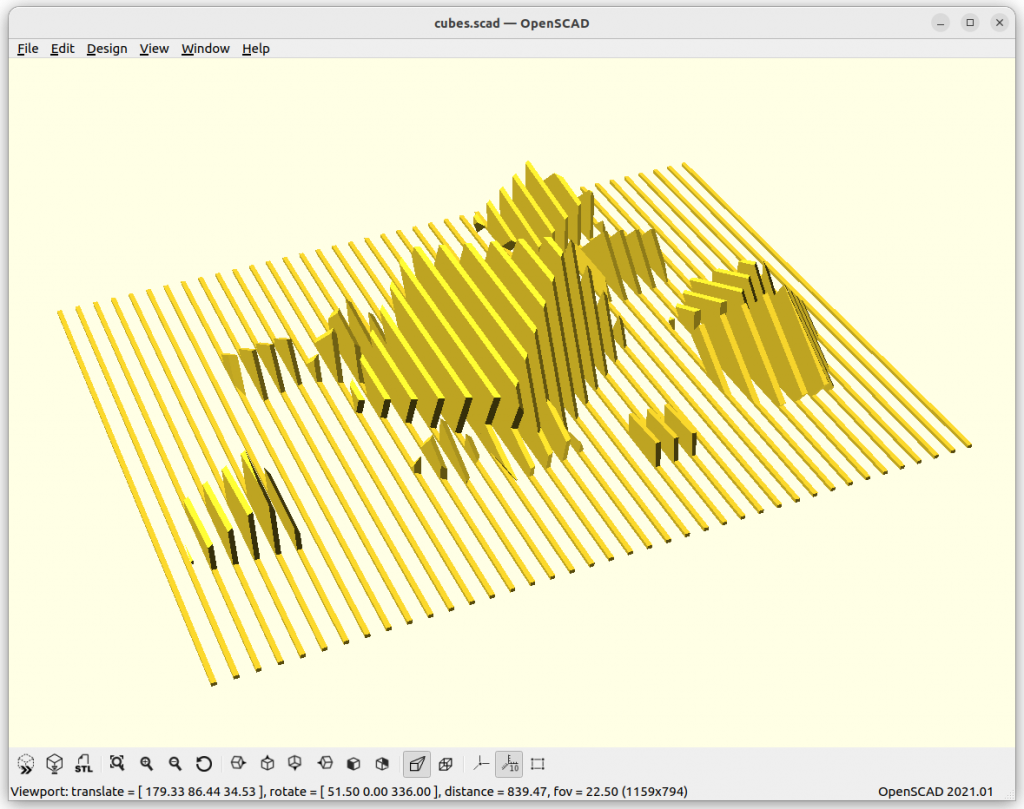
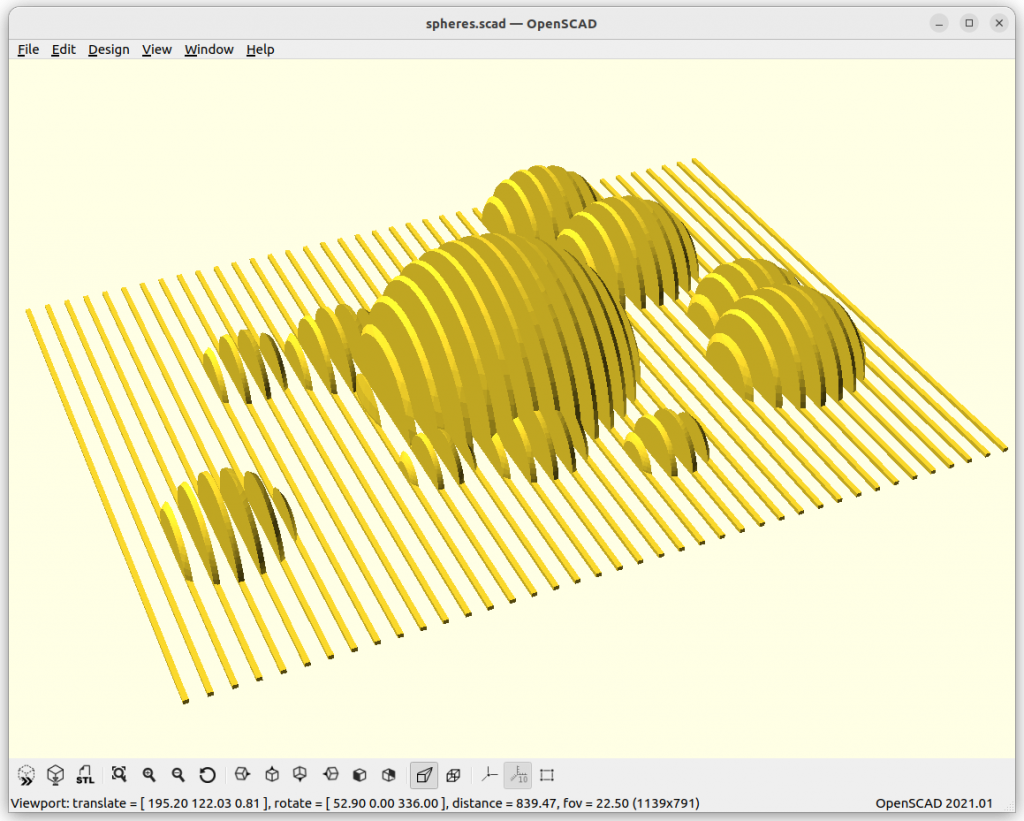
3D Printing Slices
In order to test the concept, I used 3D printed slices printed with cold-white PLA+ in order to get a strong contrasts to the black canvas:
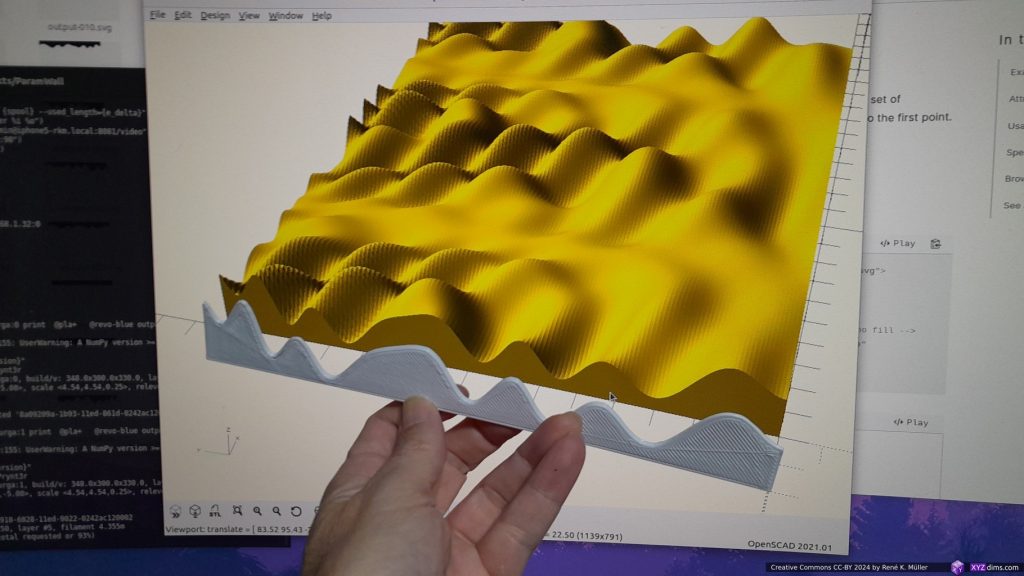
Each slice is 240mm wide, and 2.5mm thick and various height depending on the model.
After printing 40 slices finished, I mounted them on the canvas:

As shown on the photo, I used a mounting tool / rulers, also 3D printed, which helped me to keep the slices well aligned and spaced to each other – then glued each slice on the canvas.
40 slices with 240mm width and 2.5mm thickness takes about 20hrs to print (4 slices ~ 2hrs print time) and ~520g of filament like for the Sinus themed sculptures.

With 2.5mm thickness x 40 and 340mm canvas width, it’s about ~25% or 1/4 of actual volume of the model, and the rest is empty space in between.
Sinus Mountain Range




Cubes




Spheres




Smooth Sinus Meadow






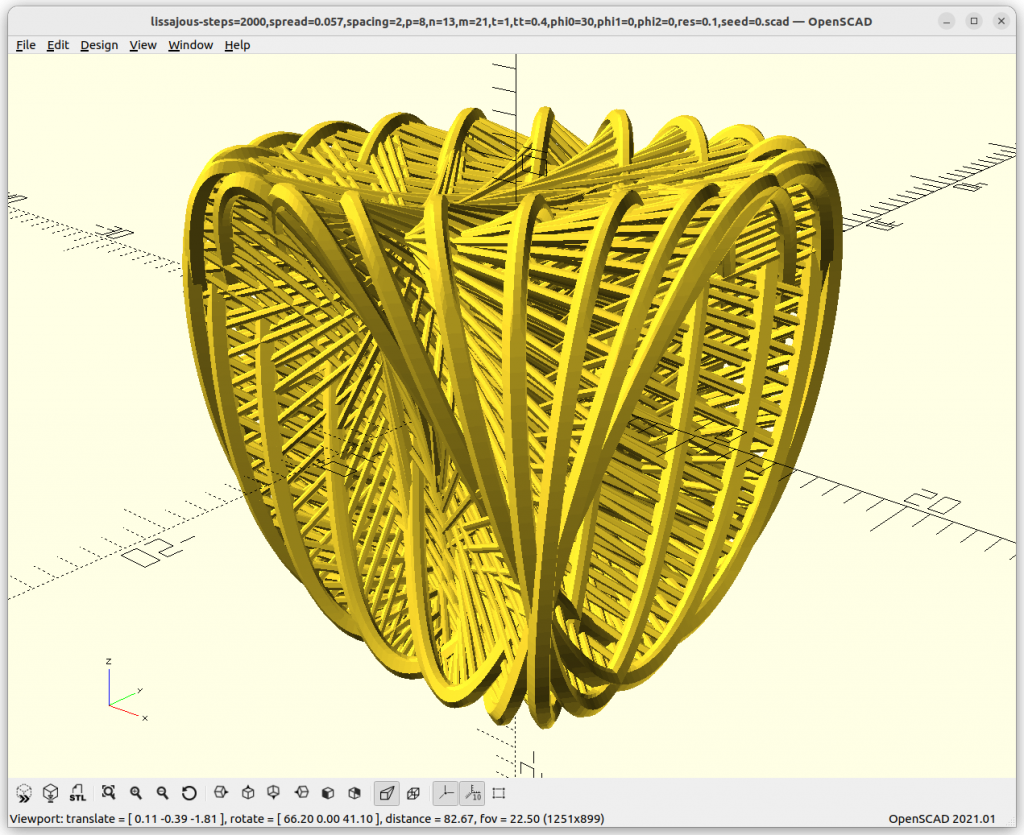
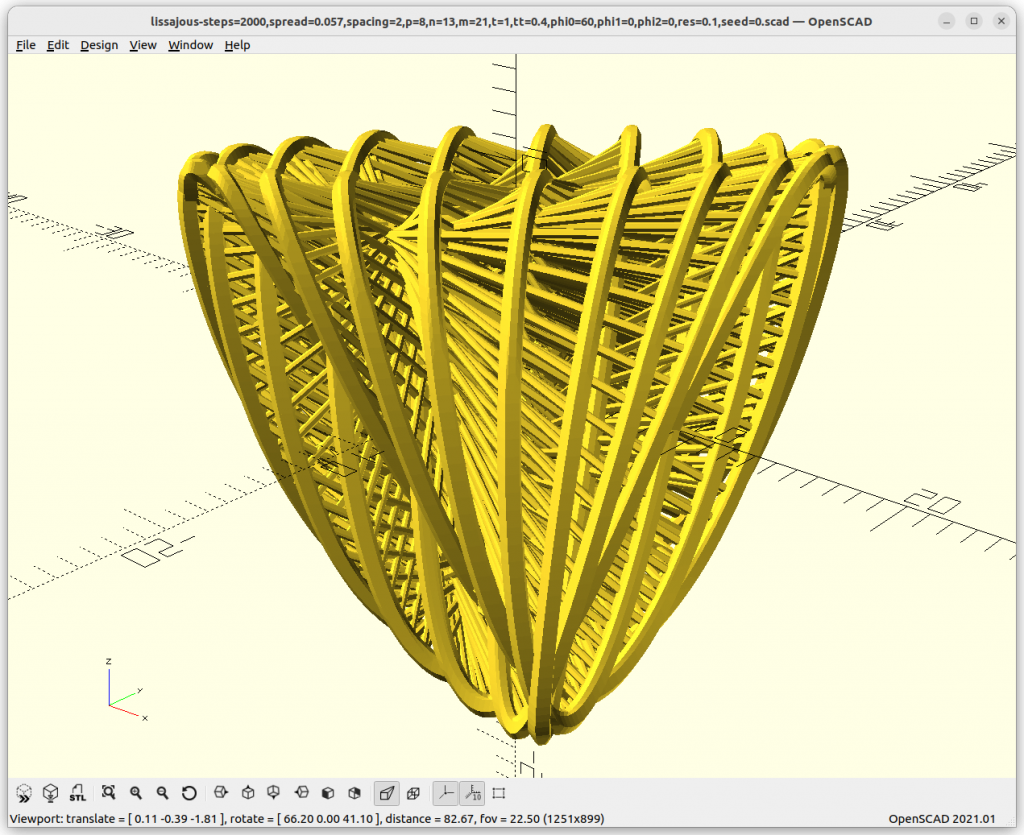
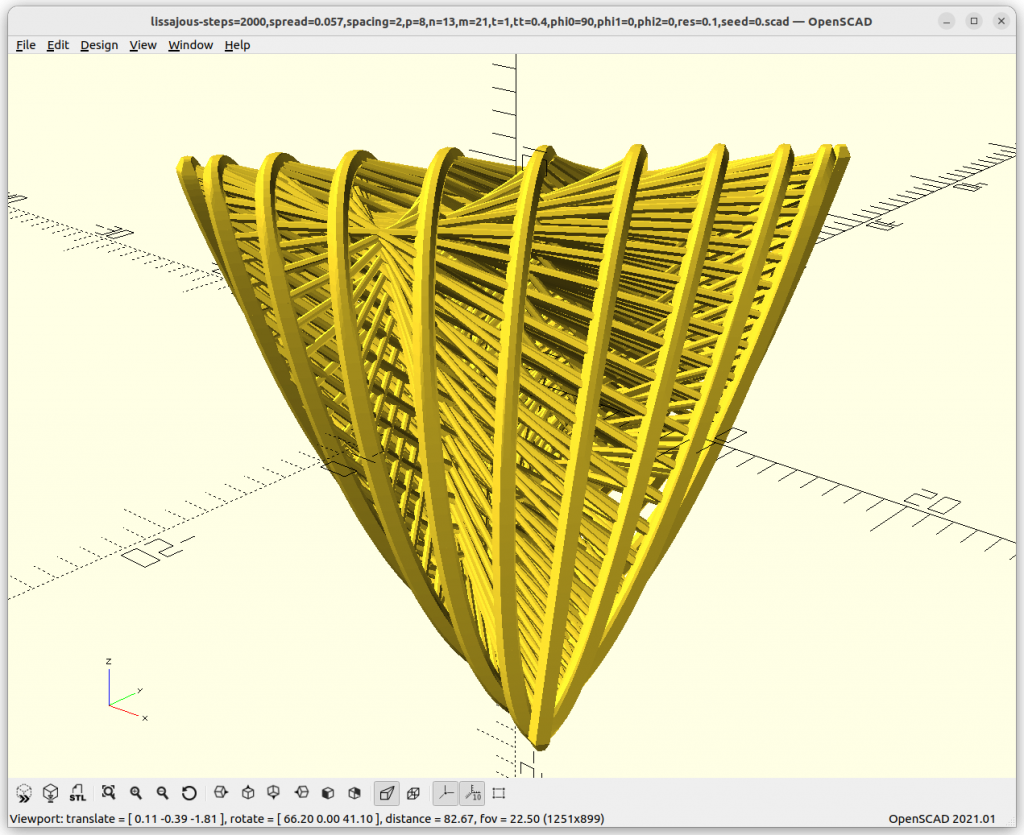
Various Examples


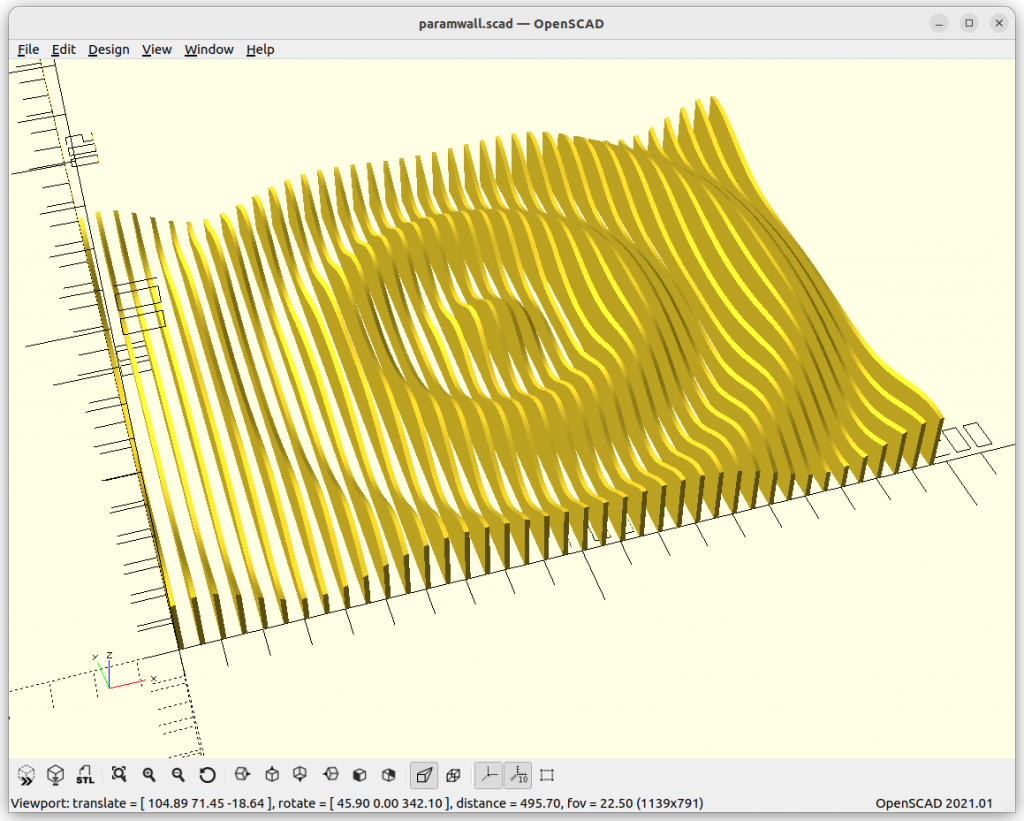


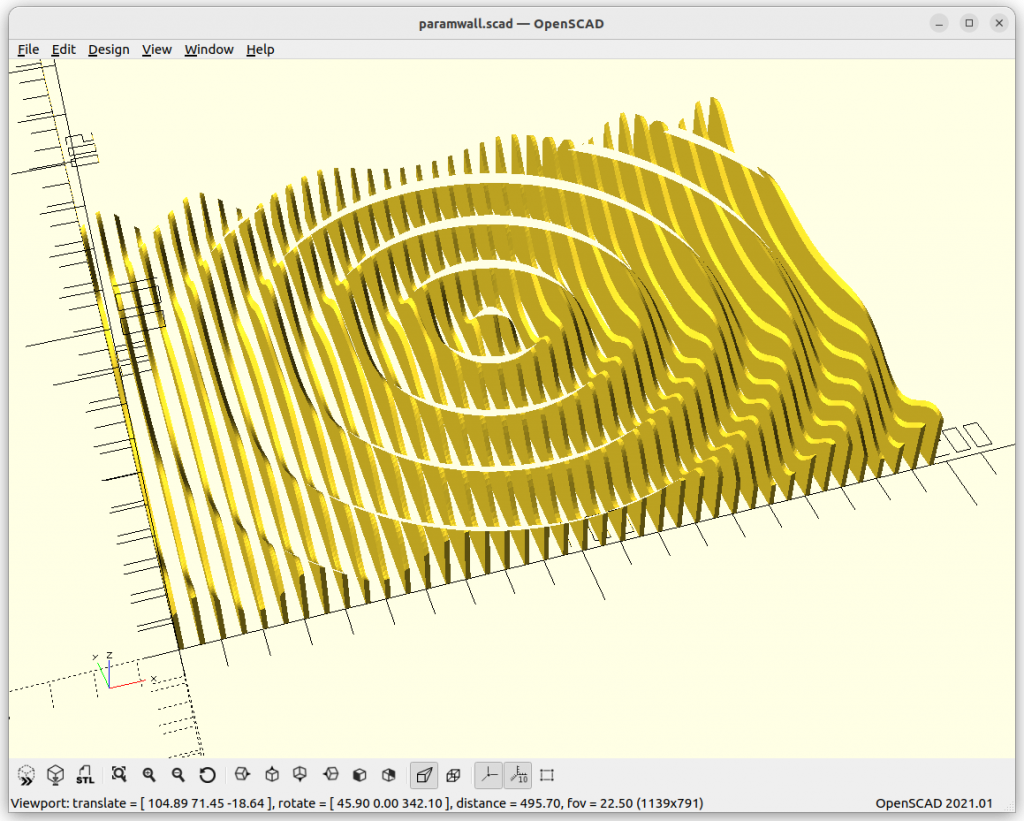


Conclusion
It’s relatively easy to create a Slices on Canvas (parametric canvas) but it takes its time to print and assemble – due the thin slices the sculpture changes its appearance drastically depending on viewing angle, and so is an eye catcher.
It certainly is a viable approach for larger scale sculptures, the saving in material is compensated with additional manual work like aligning and fastening the slices.