Updates:

• 2024/01/22: published without much reflection & conclusion as research is ongoing
• 2023/12/02: adding more examples and refining details
• 2023/10/22: start writeup

Introduction

While studying continuous fiber 3D printing and its main nature is to find ways to lay fiber without interruption. In order to refresh my memory I revisited the Lissajous forms, which until recently only knew in their 2D form, the swirling strings or lines – and now extending it into 3D as well.

The main idea is to realize how a line, string or fiber can be used to fill non-planar and circumvent a 3D structure and how angular shifting in Lissajous context affects such form.

3D Lissajous

• angle: 0 .. 2pi or 0 .. 360°
• p, n, m: 0 .. 1000, the amount of loops
• phi₀, phi₁, phi₂: the angular offsets 0 … 2pi or 0 .. 360°
• X = sin(angle*p+phi₀)*r
• Y = sin(angle*n+phi₁)*r
• Z = sin(angle*m+phi₂)*r

I did a lot of experimenting – I could post hundreds of forms – but let me focus on one a bit closer, which got my attention:

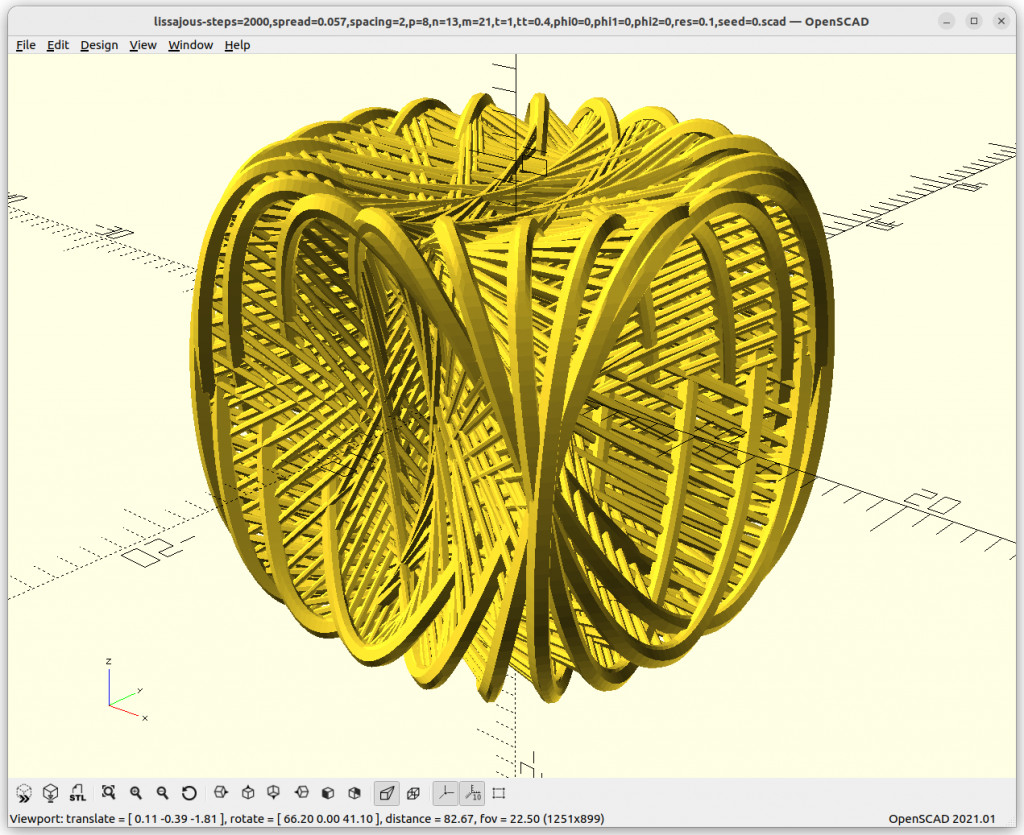
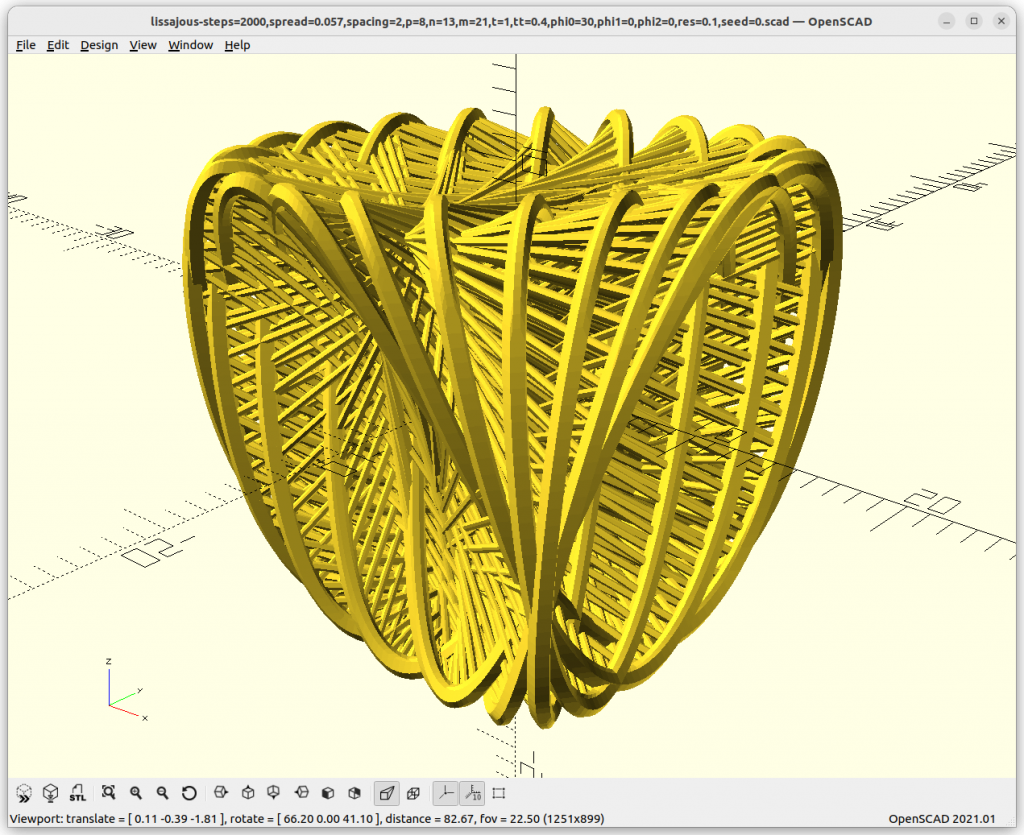
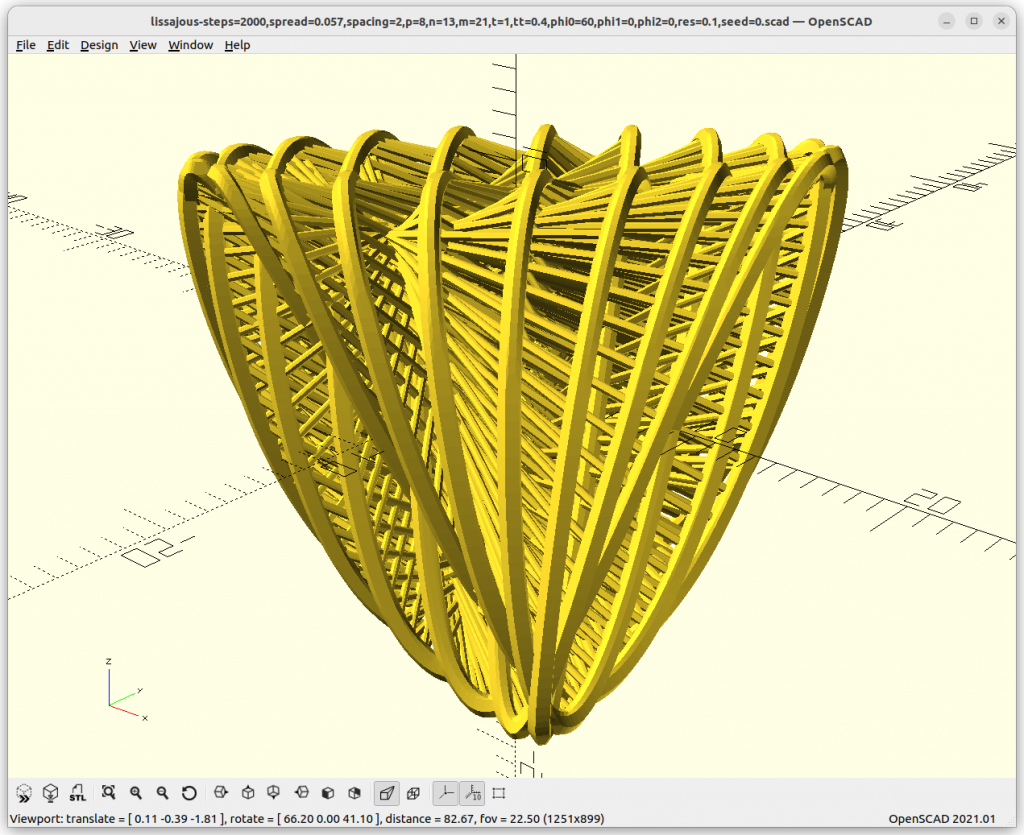
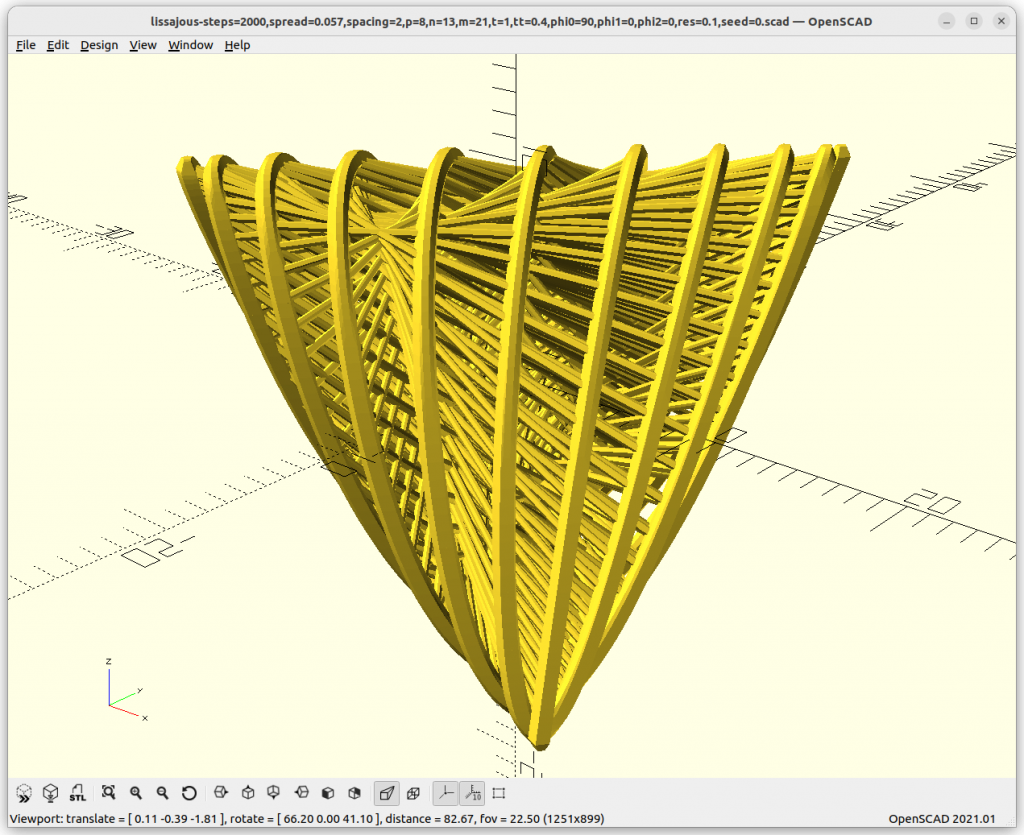
It is a very interesting transition, 8/13/21 with phi₀=0° gives almost a cube-like structure, and shifting the X loop to 90° we get a tetrahedron:

Spherical Lissajous

While playing with 3D Lissajous, I thought to adapt the cyclic nature, but apply it to a circle laying in the XY plane and then rotate in X axis, and Y axis as well, and optionally cyclic translation as well:

• d: diameter
• angle: 0 .. 2pi or 0 .. 360°
• p: amount of loops as in X=sin(angle*p)*d/2, Y=cos(angle*p)*d/2
• q: amount of X rotations: rotateX(angle*q)
• r: amount of Y rotations: rotateY(angle*r)

The model was printed with MSLA white resin at XYZ 50um resolution with 120mm diameter, with a few support structures near the bottom:

Spherical Lissajous with Translations

Using the Spherical Lissajous and extend it slightly:

• [A,B,C]loop/offset/radius: translate([ sin(angle*A_L+A_O)*A_R], sin(angle*B_L+B_O)*B_R], sin(angle*C_L+C_O)*C_R ])

which spreads the ribbons away from the spherical surface origins.

Spherical Lissajous 5.11 A_L=3, A_R=5

It’s symmetric X- and Z-wise, in Y-axis it isn’t.

The model was printed with MSLA white resin at XY 35um / Z 50um, at 60mm in Z height, ~94mm width; with a some support structures:

Spherical Lissajous 11.15 A_L=2, A_R=5

A more elaborate form is 11.15 A_L=2, A_R=5:

So, there is no X-, Y- or Z-wise symmetry.

The model was printed with MSLA white resin at XY 35um / Z 50um, at 60mm in Z height, ~94mm width; with a some support structures:

and printing it larger with ~200mm width with manually positioned support:

That’s it (for now).

References

• Wikipedia: Lissajous
• 3D Lissajous