Tag Archives: Cylinderical Slicing

3D Printing: Non-Planar Slicing with Planar Slicer

by · published Technology , , , , ,

Updates:

  • 2021/04/09: spherical slicing redone, slightly better than before
  • 2021/04/03: cylindrical & spherical slices added
  • 2021/03/26: refocusing to non-planar slicing with planar slicing
  • 2021/03/14: starting write-up with basic illustrations

Introduction

After discovering the 4-axis Rotating Tilted Nozzle (RTN) and its prototype of RotBot as developed by ZHAW and their conic slicing method, it became clear to me a 5-axis 3D printer with variable tilting nozzle is the way to go as it is a superset of 4-axis and 3-axis 3D printing.

With that in mind, I realized there was time to explore non-planar slicing with planar slicers in more details.

Slicing Methods

Let’s provide an overview of various slicing methods:

  • horizontal slice, printable on 3-, 4- and 5-axis 3D printer
  • tilted slice, 20-25° tilt printable on 3-axis, 45° tilt printable on 4- and 5-axis 3D printer
  • conical slice, 20-25° cone angle printable on 3-axis, 45° cone angle printable on 4- and 5-axis 3D printer
  • cylindrical slice, printable on rotational 3-axis printer, or 5-axis 3D printer
  • (hemi-)spherical slice, printable on 5-axis 3D printer

Horizontal Slices

Vertical slicing creates horizontal slices, the traditional aka planar slicing method, so issues and limitations are well known:

  • simple to slice
  • only challenge is to create support structure for overhangs to ensure all printed layers have layers beneath
  • no collision detection needed, as all already printed layers are beneath
  • 20mm cube
  • 20mm cube vertical sliced

Tilted Slices

Tilted slices are kind of new(er) and became known with belt printers, usually 45° tilted:

  • 20mm cube
  • 45° tilt mapped
  • 45° tilt mapped sliced
  • 20mm cube 45° tilt sliced

Transformation is [ x, y, z – y ]

  • simple to slice
  • belt-printer: no collision detection is needed
  • can print 90° overhangs in one direction only

There are patches for Cura available to slice for belt printer, additional the experimental Slicer4RTN also provides tilted slicing.

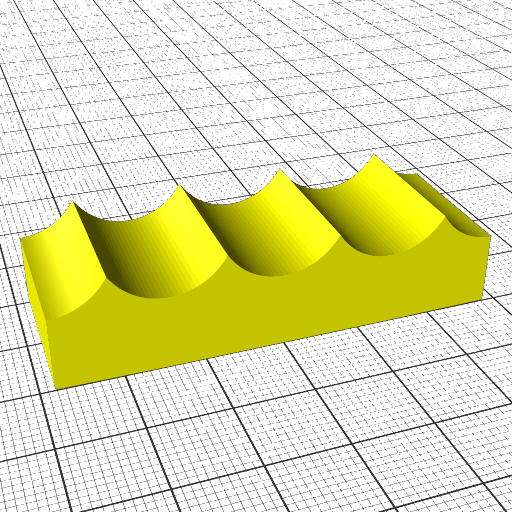
Conical Slices

New slicing method as introduced by ZHAW researchers and announced in 2021/01 utilizing planar slicer:

  • requires a center of the conic layers
  • can print 90° overhangs, two distinct modes: inside out (outside cone), or outside in (inside cone) depending on direction to a central slicing cone center
  • requires rotating and tilted nozzle aka Rotating Tilted Nozzle (RTN)
  • angle of conic slicing can be changed from 45° to 20° and models become printable with vertical nozzle with reduced print quality
  • 20mm cube
  • conic mapped
  • conic mapped sliced
  • 20mm cube conic sliced

Transformation is [ x, y, z + sqrt(x2 + y2) ]

I implemented a conic slicer named Slicer4RTN in 2021/03. There are more complex conic transformations possible, e.g. map the x/y angle via atan(y/x) but just adding sqrt(x2 + y2) to z does achieve a conic slice.

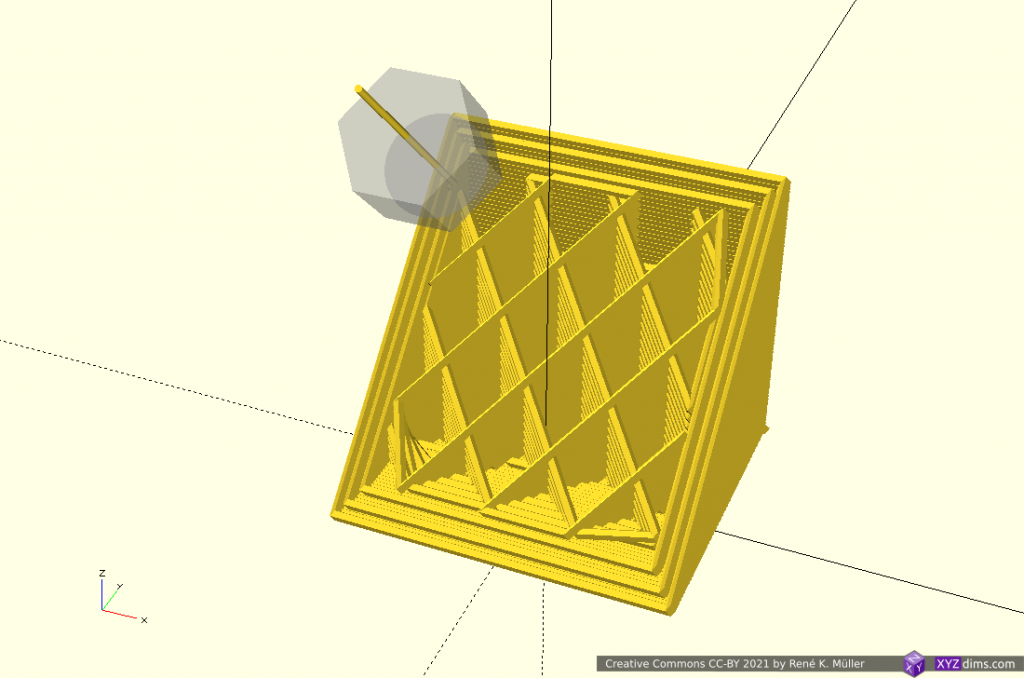
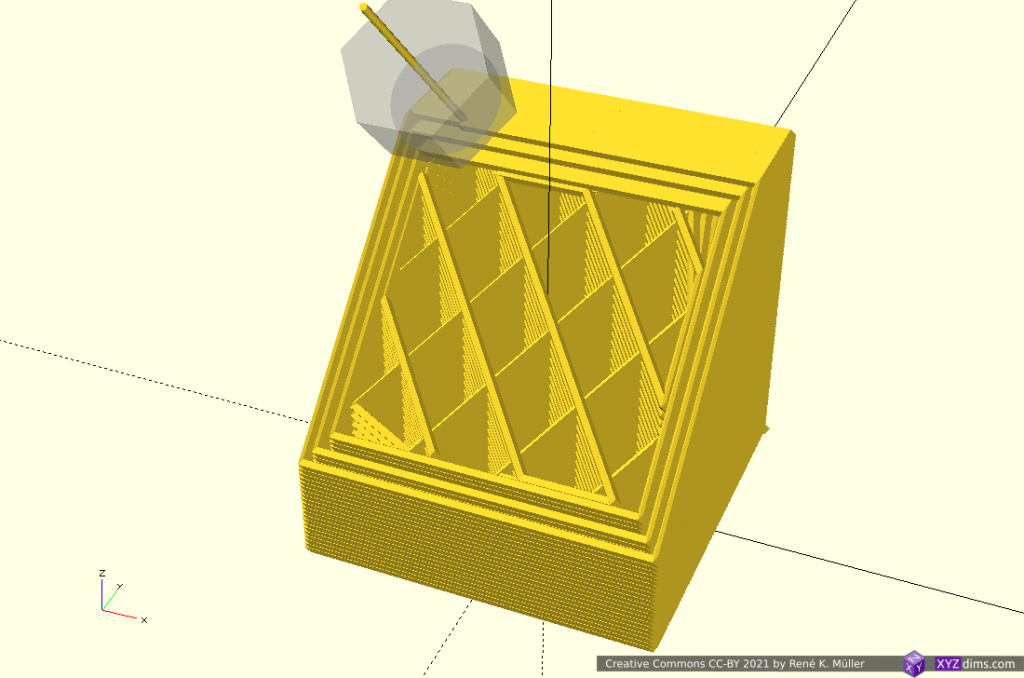
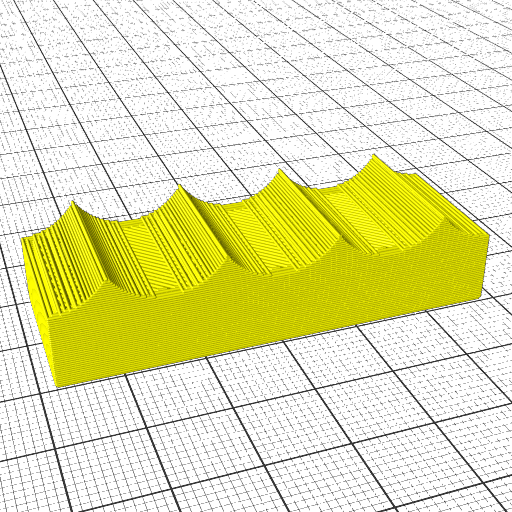
Cylindrical Slices

Early tests using planar slicers to slice also cylindrical, like this:

  • 20mm cube
  • cylinderical mapped
  • cylinderical mapped planar sliced
  • cylindrical radius corrected mapped
  • cylindrical radius corrected planar sliced
  • 20mm cube cylindrical sliced

Transformation is [ atan(y/x), z, sqrt(x2 + y2) ]

It can be printed on a fixed vertical rod, with a rotating and tilting nozzle, or horizontal rotating rod (like a lathe) and vertical nozzle then:

I came up with this way by myself based on the study on conic(al) slicing but I was made aware researchers Coupek, Friedrich, Battran, Riedel back in 2018 published a paper on this method already.

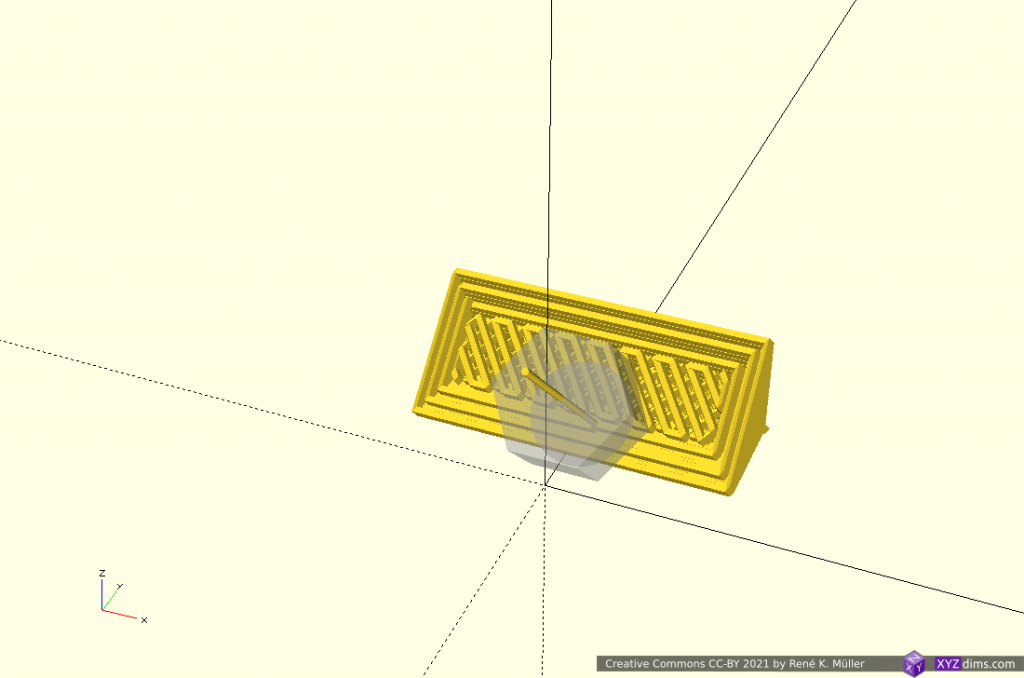
(Hemi-)Spherical Slices

Early tests using planar slicers to slice also spherical, like this:

  • 20mm cube
  • spherical mapped
  • spherical mapped planar sliced
  • spherical radius corrected mapped
  • spherical radius corrected planar sliced
  • 20mm cube spherical sliced

Transformation is [ sqrt(x2 + y2 + z2), atan(y/x), atan(z/sqrt(x2 + y2)) ]

It can be printed with a 5-axis like PAX printhead, it’s main advantage is to getting close to print continuous overhangs of any angle.

I suspect at least one more suitable and simpler sphere transformation, as soon I came up with such I add it on this blog-post.

Conclusion

It is possible to slice non-planar with planar slicers by mapping to and from the space of the slicing you like to have; yet in the slicing procedure some margins are introduced which need to be compensated – the planar slicer needs to work reliable, Slic3r 1.2.9 and CuraEngine 4.4.1 / cura-slicer perform reliable, whereas PrusaSlicer 2.1.1 makes assumptions of the printability and exits when no printable G-code can be produced, not recommended for this case therefore.

The simpler the transformation forward and backward, the more precise G-code can be obtained, e.g. tilted and conic slices provide precise G-code, whereas cylindrical and spherical slices are harder to tune with the planar slicer.

  • Planar sliced 20mm cube
  • Tilt sliced 20mm cube
  • Conic sliced 20mm cube
  • Cylindrical sliced 20mm cube
  • Spherical sliced 20mm cube

References